이번 강의는 그래디언트 연산자 ∇ 와 미분 연산자 'd'를 비교해볼 참이다. 먼저 기초강좌의 '측량텐서의 색인 올림과 내림'편을 보고 시작하면 좋다.
-

-
그레디언트(Gradient) 또는 델(Del) 이라고 불리는 ∇ 연산자와 미분 연산자 'd'의 차이를 비교분석해 보기로 하자.
-

-
수학과 물리학 연구자들 사이에서도 이 두 연산자에 대한 혼용이 있어 학습자를 혼란 스럽게 한다. 'Gravitation' 책에는 d 연산자를 그래디언트라고 하고 있고, 위키사전에 미분형 연산자를 'exterior differential' 이라고 설명되기도 하며, 그래디언트를 미분 1형 연산자라고 기술하고 있다.
-

-
더구나 그래디언트(Gradient)는 벡터장(Vector Field)으로 취급하거나 여벡터(Covector)의 일종이라고 설명하기도 한다.
-

-
'혼용' 되고 있다 해서 틀린 것은 아니다. 다만, 혼동을 피하기 위해 이 강의에서는 다음과 같이 쓰기로 한다. 특히, df 에 '그래디언트'란 용어를 적용하는 것은 피한다. 그래디언트는 델 연산자를 지칭하는 것으로 하자.
-

-
'델' 과 'd' 모두 스칼라장(scalar field) 함수 f() 에 적용되는 연산자다. 델 연산자는 스칼라장에 작용하여 벡터장을 만들어내고 d 연산자는 여벡터장을 만들어 낸다. 이 여백터장을 1-형(1-form)이라고 한다.
이렇게 만들어진 벡터장과 여벡터장의 방향은 동일하다. 스칼라 값이 급격히 변하는 중심부의 벡터 길이가 긴데 비해 여벡터장의 등위선 간격은 좁다. 여벡터 등위선 간격이 넓은 곳의 벡터장에서 벡터길이는 짧다. [여벡터, 등위선 간격이 좁을 수록 기저 벡터가 통과하는 등위선의 갯수는 많아진다.]
-

-
두 연산자의 역활은 다르지만 비슷한 면도 가지고 있다. 이 두 연산자의 관계에 대해 알아보자.
'텐서의 기초' 강좌의 '색인 올리기와 내리기' 편에서 벡터공간(Vector Space)과 이중벡터 공간(Dual Space)사이의 특별한 관계에 대하여 배웠다. 벡터공간의 원소인 벡터 v와 이중공간의 '벡터 v 스칼라곱'(v⋅_ ; v dot something)은 서로 대응관계에 있다. 이중공간의 v⋅_ 은 연산자로서 다른 벡터를 필요로 하며 연산의 결과는 스칼라다.
-

-
∇f 와 df 사이에도 비슷한 관계를 맺을 수 있다. 어떤 관계가 되는지 알아보자.
-

-----------------------------------------------------------------------
'그래디언트'의 수학적 정의 [참조]
스칼라 함수  의 기울기는
의 기울기는  로 표현한다.
로 표현한다.  기호는 벡터 미분 연산자로 나블라(nabla) 혹은 델(del)연산자라고 부른다. 그래디언트(기울기는)
기호는 벡터 미분 연산자로 나블라(nabla) 혹은 델(del)연산자라고 부른다. 그래디언트(기울기는)  의 각 성분의 편미분으로 구성된 열벡터로 정의하며 다음과 같이 표시한다.
의 각 성분의 편미분으로 구성된 열벡터로 정의하며 다음과 같이 표시한다.

직교좌표계라면,

 이다.
이다.
* '델' 연산자를 그자체로 벡터장과 혼용 되어 사용하거나 스칼라 함수를 벡터화 해주는 연산자라 하기도 한다. 어쨌든 스칼라 함수를 벡터로 변환 시켜준다.
[참조: 6. 차분형은 여벡터(Differential Forms are Covectors)]
-
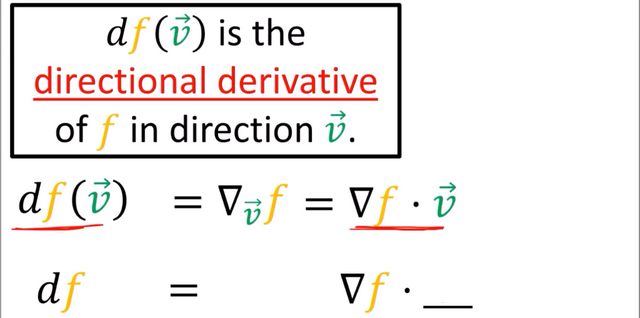
-
따라서 다음과 같은 관계에 있다. ∇f 를 벡터장(Vector Field)이라 한다면 df를 '이중' 여벡터장(Covector Field)이라고 한다.
-

-
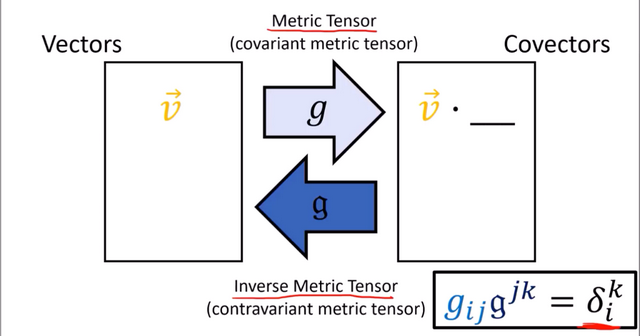
색인 올림과 내림 강의에서 벡터와 여벡터 사이에 측량텐서(Metric Tensor)를 통해 변환이 가능 하다는 것을 배웠다. 그리고 그 반대의 경우는 역 측량텐서(Inverse Metric Tensor)를 이용한다. 그리고 측량텐서와 역 측량텐서의 곱은 단위행렬(=크로네커 델타)이다.
-
-
두 벡터의 스칼라 곱은 측량텐서와 벡터의 성분 곱이 되는 사실은 쉽게 증명할 수 있다.
-

-
따라서, 벡터 스칼라 곱 , v⋅_ 는 벡터 v 의 성분과 측량텐서의 곱에 곱해질 벡터의 기저 여벡터 ε^j 를 곱한 것과 같다.
-

-
벡터 스칼라 곱 v⋅_ 이 여벡터이므로 v의 성분과 측량텐서의 곱은 기저 여벡터의 성분이다.
-

-
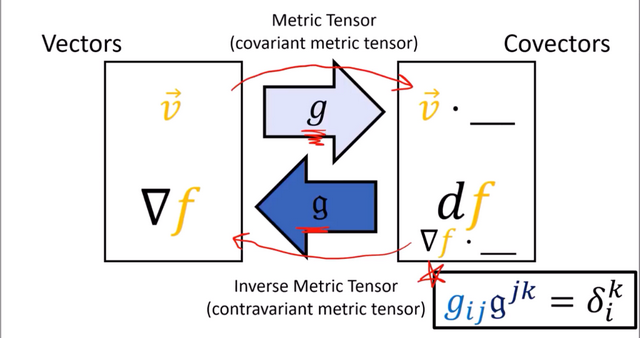
측량텐서를 사용하여 벡터와 여벡터 사이의 변환이 가능한 것과 마찬가지로 벡터장과 여벡터장의 변환도 동일하게 적용할 수 있다.
-
-
측량텐서를 이용하여 벡터장과 여벡터장 사이의 변환 관계를 증명하면 다음과 같다. [ df(v)는 벡터를 이용해 여벡터 장을 측정하는 방법임]
[1] 벡터 v 의 스칼라 함수 미분형, df(v) 은 스칼라 함수의 그래디언트 ∇f 와 벡터 v의 스칼라 곱이 됨을 증명
[2] (∇f)^i =∂f/∂(x^i) i-번째 기저축 편미분은 기저벡터 e_i의 성분
[3] 두 벡터의 성분의 곱, ((∇f)^i )(v^j)
[4] 기저벡터 스칼라 곱은 측량텐서
[5] 스칼라 함수 f에 대한 미분 연산자와 그래디언트 스칼라 곱은 기저 여벡터와 성분의 선형 확장형
[6] (v^j) 와 d(c^j) 의 등가 관계는 다음편 강의에서 설명할 것임
-

-
[1] 양변에 모두 기저 여벡터 d(c^j)를 담고 있다.
[2] 이는 여벡터장의 성분 ∂f/∂(c^i) 과 스칼라 함수의 f의 그래디언트 성분(=벡터장의 성분)과 측량텐서 곱이 서로 대응하는 관계에 있다는 것을 보여준다.
-

-
벡터장 성분(Vector field components)에 측량 텐서를 곱하여 여벡터장 성분(Covector field components)으로 변환될 수 있음을 보여준다.
-

-
역 측량텐서의 정의를 적용하여 여벡터장 성분에서 벡터장 성분으로 역변환 할 수 있다.
-

-
따라서 벡터장과 여벡터장 사이의 변환 관계는 측량텐서와 역측량텐서를 통하면 상호 변환 할 수 있다. [측량 텐서의 역활에 주목하자.]
-

-
흥미로운 점은 스칼라 함수의 그래디언트, ∇f 는 위의 역 측량텐서 변환 식을 적용하면 다음과 같이 표현될 수 있다. [∇f는 벡터장이다.]
-

-
결국 벡터장(Vector field) ∇f 은 역 측량텐서와 스칼라 장의 편미분 곱을 성분으로 하는 기저벡터의 선형합으로 표현된다. 그래디언트를 표현하는 여러 방법이 있으나 그중 역 측량텐서가 포함된 경우는 아주 흥미롭다.
-

-
정규직교좌표계의 경우 측량텐서와 역측량 텐서 모두 크로네커 델타와 같다. 따라서 ∇f 의 확장 표현에 역 측량 텐서를 이용해 확장되었다 해도 특이할 것이 없다.
-

-
이번에는 극좌표의 경우를 보자. 앞선 강의(11편)에서 구했던 역측량텐서를 활용하여 ∇f 를 확장해보자.
역측량텐서의 대각 성분 외에는 0이다. 따라서 (r,r) 성분은 1, (θ,θ) 성분은 1/(r^2)다.
따라서 극좌표에 대한 ∇f의 확장 표현은 다음과 같다.
-

-
여기서 한가지 주의할 사항은 이 강의에서는 극좌표계를 정규화되지 않은(Non-Normalized) 기저벡터로 정의하였다는 점이다. 따라서 일반적인 교과서에 나온 성분 표현과 차이가 있다는 점을 밝혀둔다.
-

-
중요한 점은 스칼라 그래디언드(혹은 벡터장) ∇f 은 기저축으로 편미분을 성분으로 삼아 기저벡터의 곱의 선형합으로 확장 표현 할 수 있다는 점이다. 다만 좌표계에 따라 추가된 항이 있다는 점에 유의하자. 이 벡터장의 선형확장 표현은 여벡터장에서 벡터장으로 성분 변환식(역 측량텐서 곱)으로부터 나왔다.
-

-
[벡터의 확장표현은 성분과 기저벡터 곱의 선형 합이다. 이는 좌표계가 변환 되어도 같은 방식의 확장 표현이 성립된다. 하지만 벡터장의 경우 좌표계에 따라 추가된 항이 존재한다. 위의 예에서 극좌표계의 경우 각도축 기저벡터에 1/r 항이 더 곱해지고 있다. 이는 좌표계에 따라 기저축의 왜곡되기도 한다는 것을 보여준다.]
-
정규직교 좌표계만이 벡터장과 여벡터장의 성분이 동일하다.
-

-
극좌표의 경우 벡터장 확장표현에 추가된 항이 곱해진다. 각도축에 1/r이 추가로 곱해지는데 단순해서 다행이다.
-

-
구면 좌표계(Spherical coordinate)라면 그래디언트의 확장은 다소 복잡해진다. 이 추가된 항들은 역시 역측량텐서로부터 기인한다.
구면좌표계의 그래디언트 표현은 다변수 미적분 과목에서도 배운다. 이 식을 유도하기 위해 여러번의 치환과정을 거쳐야 하지만 텐서 미적분에서는 그저 역 측량텐서만 알면 쉽게 풀 수 있다.
-

-
요약: 스칼라장 함수 f에 [스칼라장 함수의 매개변수 변화: f(x,y) -> (x(t), y(t)) -> f(t)]
1. 그래디언트를 취하면 벡터장의 표현이된다. [그래디언트를 벡터화 도구라 한다].
2. 미분 연산자를 취하면 여벡터장이 된다.
-

-
벡터장과 여벡터장 사이의 대응관계는 벡터와 여벡터의 경우와 같다.
-

-
벡터장과 그에 대응하는 여벡터장 사이의 성분 변환은 측량텐서(역측량텐서)의 곱을 통해 이뤄진다.
-

-
벡터장과 여벡터장 사이의 성분 변환 공식
-

-
공식외우기:
측량텐서를 곱해서 색인 내리기 => 여벡터장 성분 (Co-Variant)
역측량텐서를 곱해서 색인 올리기 => 벡터장 성분 (Contra-Variant)
-

----------------------------------------------------------------
 의 기울기는
의 기울기는  로 표현한다.
로 표현한다.  기호는 벡터 미분 연산자로 나블라(nabla) 혹은 델(del)연산자라고 부른다. 그래디언트(기울기는)
기호는 벡터 미분 연산자로 나블라(nabla) 혹은 델(del)연산자라고 부른다. 그래디언트(기울기는)  의 각 성분의 편미분으로 구성된 열벡터로 정의하며 다음과 같이 표시한다.
의 각 성분의 편미분으로 구성된 열벡터로 정의하며 다음과 같이 표시한다.
직교좌표계라면,

예를 들어 함수,  의 그래디언트는
의 그래디언트는
 의 그래디언트는
의 그래디언트는 이다.
이다.* '델' 연산자를 그자체로 벡터장과 혼용 되어 사용하거나 스칼라 함수를 벡터화 해주는 연산자라 하기도 한다. 어쨌든 스칼라 함수를 벡터로 변환 시켜준다.
-----------------------------------------------------------------------
벡터의 함수 f(v)에 대한 미분 연산 df(v)를 함수 f의 방향성 미분(directional derivative, f()는 스칼라 함수 이지만 입력으로 벡터를 취한다. 벡터는 값과 '방향'을 가지고 있다.) 이라고 하며 아래와 같이 표기한다. 이는 스칼라 함수 f 를 델 연산으로 벡터화 하여 v 와 스칼라 곱한 것과 같다. [스칼라 곱은 벡터와 벡터 사이에 연산할 수 있으므로][참조: 6. 차분형은 여벡터(Differential Forms are Covectors)]
-
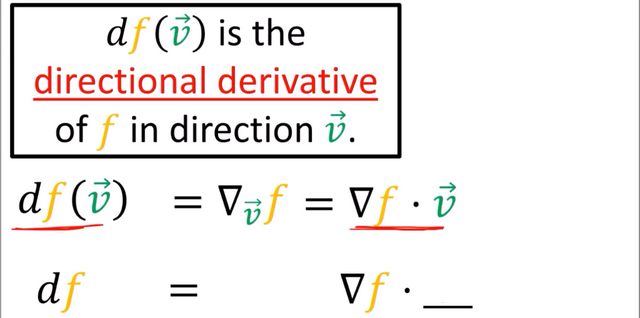
-
따라서 다음과 같은 관계에 있다. ∇f 를 벡터장(Vector Field)이라 한다면 df를 '이중' 여벡터장(Covector Field)이라고 한다.
-

-
색인 올림과 내림 강의에서 벡터와 여벡터 사이에 측량텐서(Metric Tensor)를 통해 변환이 가능 하다는 것을 배웠다. 그리고 그 반대의 경우는 역 측량텐서(Inverse Metric Tensor)를 이용한다. 그리고 측량텐서와 역 측량텐서의 곱은 단위행렬(=크로네커 델타)이다.
-

-
두 벡터의 스칼라 곱은 측량텐서와 벡터의 성분 곱이 되는 사실은 쉽게 증명할 수 있다.
-

-
따라서, 벡터 스칼라 곱 , v⋅_ 는 벡터 v 의 성분과 측량텐서의 곱에 곱해질 벡터의 기저 여벡터 ε^j 를 곱한 것과 같다.
-

-
벡터 스칼라 곱 v⋅_ 이 여벡터이므로 v의 성분과 측량텐서의 곱은 기저 여벡터의 성분이다.
-

-
측량텐서를 사용하여 벡터와 여벡터 사이의 변환이 가능한 것과 마찬가지로 벡터장과 여벡터장의 변환도 동일하게 적용할 수 있다.
-

-
측량텐서를 이용하여 벡터장과 여벡터장 사이의 변환 관계를 증명하면 다음과 같다. [ df(v)는 벡터를 이용해 여벡터 장을 측정하는 방법임]
[1] 벡터 v 의 스칼라 함수 미분형, df(v) 은 스칼라 함수의 그래디언트 ∇f 와 벡터 v의 스칼라 곱이 됨을 증명
[2] (∇f)^i =∂f/∂(x^i) i-번째 기저축 편미분은 기저벡터 e_i의 성분
[3] 두 벡터의 성분의 곱, ((∇f)^i )(v^j)
[4] 기저벡터 스칼라 곱은 측량텐서
[5] 스칼라 함수 f에 대한 미분 연산자와 그래디언트 스칼라 곱은 기저 여벡터와 성분의 선형 확장형
[6] (v^j) 와 d(c^j) 의 등가 관계는 다음편 강의에서 설명할 것임
-

-
[1] 양변에 모두 기저 여벡터 d(c^j)를 담고 있다.
[2] 이는 여벡터장의 성분 ∂f/∂(c^i) 과 스칼라 함수의 f의 그래디언트 성분(=벡터장의 성분)과 측량텐서 곱이 서로 대응하는 관계에 있다는 것을 보여준다.
-

-
벡터장 성분(Vector field components)에 측량 텐서를 곱하여 여벡터장 성분(Covector field components)으로 변환될 수 있음을 보여준다.
-

-
역 측량텐서의 정의를 적용하여 여벡터장 성분에서 벡터장 성분으로 역변환 할 수 있다.
-

-
따라서 벡터장과 여벡터장 사이의 변환 관계는 측량텐서와 역측량텐서를 통하면 상호 변환 할 수 있다. [측량 텐서의 역활에 주목하자.]
-

-
흥미로운 점은 스칼라 함수의 그래디언트, ∇f 는 위의 역 측량텐서 변환 식을 적용하면 다음과 같이 표현될 수 있다. [∇f는 벡터장이다.]
-

-
결국 벡터장(Vector field) ∇f 은 역 측량텐서와 스칼라 장의 편미분 곱을 성분으로 하는 기저벡터의 선형합으로 표현된다. 그래디언트를 표현하는 여러 방법이 있으나 그중 역 측량텐서가 포함된 경우는 아주 흥미롭다.
-

-
정규직교좌표계의 경우 측량텐서와 역측량 텐서 모두 크로네커 델타와 같다. 따라서 ∇f 의 확장 표현에 역 측량 텐서를 이용해 확장되었다 해도 특이할 것이 없다.
-

-
이번에는 극좌표의 경우를 보자. 앞선 강의(11편)에서 구했던 역측량텐서를 활용하여 ∇f 를 확장해보자.
역측량텐서의 대각 성분 외에는 0이다. 따라서 (r,r) 성분은 1, (θ,θ) 성분은 1/(r^2)다.
따라서 극좌표에 대한 ∇f의 확장 표현은 다음과 같다.
-

-
여기서 한가지 주의할 사항은 이 강의에서는 극좌표계를 정규화되지 않은(Non-Normalized) 기저벡터로 정의하였다는 점이다. 따라서 일반적인 교과서에 나온 성분 표현과 차이가 있다는 점을 밝혀둔다.
-

-
중요한 점은 스칼라 그래디언드(혹은 벡터장) ∇f 은 기저축으로 편미분을 성분으로 삼아 기저벡터의 곱의 선형합으로 확장 표현 할 수 있다는 점이다. 다만 좌표계에 따라 추가된 항이 있다는 점에 유의하자. 이 벡터장의 선형확장 표현은 여벡터장에서 벡터장으로 성분 변환식(역 측량텐서 곱)으로부터 나왔다.
-

-
[벡터의 확장표현은 성분과 기저벡터 곱의 선형 합이다. 이는 좌표계가 변환 되어도 같은 방식의 확장 표현이 성립된다. 하지만 벡터장의 경우 좌표계에 따라 추가된 항이 존재한다. 위의 예에서 극좌표계의 경우 각도축 기저벡터에 1/r 항이 더 곱해지고 있다. 이는 좌표계에 따라 기저축의 왜곡되기도 한다는 것을 보여준다.]
-
정규직교 좌표계만이 벡터장과 여벡터장의 성분이 동일하다.
-

-
극좌표의 경우 벡터장 확장표현에 추가된 항이 곱해진다. 각도축에 1/r이 추가로 곱해지는데 단순해서 다행이다.
-

-
구면 좌표계(Spherical coordinate)라면 그래디언트의 확장은 다소 복잡해진다. 이 추가된 항들은 역시 역측량텐서로부터 기인한다.
구면좌표계의 그래디언트 표현은 다변수 미적분 과목에서도 배운다. 이 식을 유도하기 위해 여러번의 치환과정을 거쳐야 하지만 텐서 미적분에서는 그저 역 측량텐서만 알면 쉽게 풀 수 있다.
-

-
요약: 스칼라장 함수 f에 [스칼라장 함수의 매개변수 변화: f(x,y) -> (x(t), y(t)) -> f(t)]
1. 그래디언트를 취하면 벡터장의 표현이된다. [그래디언트를 벡터화 도구라 한다].
2. 미분 연산자를 취하면 여벡터장이 된다.
-

-
벡터장과 여벡터장 사이의 대응관계는 벡터와 여벡터의 경우와 같다.
-

-
벡터장과 그에 대응하는 여벡터장 사이의 성분 변환은 측량텐서(역측량텐서)의 곱을 통해 이뤄진다.
-

-
벡터장과 여벡터장 사이의 성분 변환 공식
-

-
공식외우기:
측량텐서를 곱해서 색인 내리기 => 여벡터장 성분 (Co-Variant)
역측량텐서를 곱해서 색인 올리기 => 벡터장 성분 (Contra-Variant)
-

----------------------------------------------------------------
[이전] 12.곡면에서 원호길이 측량(The Metric Tensor in Curved Spaces for Measuring Arc Length)
[다음] 14. 벡터장 추가설명 및 예제(Gradient explanation & examples)
----------------------------------------------------------------
강의목차:
Tensor Calculus by eigenchris @ Youtube
0. 소개(Introduction)
1. 다변수 미적분 요약(Multi-variable Calculus Review)
2. 직각좌표계와 극좌표계 그리고 기저벡터(Cartesian & Polar ㅌCoordinates, and Basis Vectors)
3. 자코비언(The Jacobian)
4. 미분하면 벡터된다(Derivatives are Vectors)
5. Derivative Transformation Rules (Contravariance)
5.1 Derivative Operators are Vectors Discussion
6. 차분형은 여벡터(Differential Forms are Covectors)
7. 여벡터 장 성분(Covector Field Components)
8. 8. 여벡터장 변환규칙(공변)(Covector Field Transformation Rules (Covariance))
9. 차분형(여벡터장) 적분[경로적분](Integration with Differential Forms)
10. 차분형 적분[경로적분] 예제(Integration with Differential Forms Examples)
11. 측량텐서와 원호길이(평면)(The Metric Tensor and Arc Lengths (flat space))
12. 곡면에서 원호길이 측량(The Metric Tensor in Curved Spaces for Measuring Arc Length)
13. 그래디언트 ∇ 와 미분연산자 'd' (Gradient vs 'd' operator)
14. 벡터장 추가설명 및 예제(Gradient explanation & examples)
15. Geodesics and Christoffel Symbols (extrinsic geometry)
16. Geodesic Examples on Plane and Sphere
17. The Covariant Derivative (flat space)
17.5 Covariant Derivative (Component Definition) - Optional
18. Covariant Derivative (extrinsic) and Parallel Transport
19. Covariant Derivative (Intrinsic) and Geodesics
20. The Abstract Covariant Derivative (Levi-Civita Connection)
21. Lie Bracket, Flow, Torsion Tensor
22. Riemann Curvature Tensor Geometric Meaning (Holonomy + Geodesic Deviation)
23. Riemann Curvature Tensor Components and Symmetries
24. Ricci Tensor Geometric Meaning (Sectional Curvature)
25. Geometric Meaning Ricci Tensor_Scalar (Volume Form)
26. Ricci Tensor_Scalar Properties
[다음] 14. 벡터장 추가설명 및 예제(Gradient explanation & examples)
----------------------------------------------------------------
강의목차:
Tensor Calculus by eigenchris @ Youtube
0. 소개(Introduction)
1. 다변수 미적분 요약(Multi-variable Calculus Review)
2. 직각좌표계와 극좌표계 그리고 기저벡터(Cartesian & Polar ㅌCoordinates, and Basis Vectors)
3. 자코비언(The Jacobian)
4. 미분하면 벡터된다(Derivatives are Vectors)
5. Derivative Transformation Rules (Contravariance)
5.1 Derivative Operators are Vectors Discussion
6. 차분형은 여벡터(Differential Forms are Covectors)
7. 여벡터 장 성분(Covector Field Components)
8. 8. 여벡터장 변환규칙(공변)(Covector Field Transformation Rules (Covariance))
9. 차분형(여벡터장) 적분[경로적분](Integration with Differential Forms)
10. 차분형 적분[경로적분] 예제(Integration with Differential Forms Examples)
11. 측량텐서와 원호길이(평면)(The Metric Tensor and Arc Lengths (flat space))
12. 곡면에서 원호길이 측량(The Metric Tensor in Curved Spaces for Measuring Arc Length)
13. 그래디언트 ∇ 와 미분연산자 'd' (Gradient vs 'd' operator)
14. 벡터장 추가설명 및 예제(Gradient explanation & examples)
15. Geodesics and Christoffel Symbols (extrinsic geometry)
16. Geodesic Examples on Plane and Sphere
17. The Covariant Derivative (flat space)
17.5 Covariant Derivative (Component Definition) - Optional
18. Covariant Derivative (extrinsic) and Parallel Transport
19. Covariant Derivative (Intrinsic) and Geodesics
20. The Abstract Covariant Derivative (Levi-Civita Connection)
21. Lie Bracket, Flow, Torsion Tensor
22. Riemann Curvature Tensor Geometric Meaning (Holonomy + Geodesic Deviation)
23. Riemann Curvature Tensor Components and Symmetries
24. Ricci Tensor Geometric Meaning (Sectional Curvature)
25. Geometric Meaning Ricci Tensor_Scalar (Volume Form)
26. Ricci Tensor_Scalar Properties
댓글 없음:
댓글 쓰기