'미분하면 벡터'가 되는 원리를 배웠다. 이번 편은 그 미분의 변환 법칙을 공부한다. '텐서의 기초' 강좌중 '3. 벡터변환 규칙(Vector Transformation Rules)'을 먼저 보면 좋다.
-
-
이전 강의를 복습 해보자. ['미분하면 벡터'의 엄밀한 의미는 공간에서 움직이는 벡터의 궤적을 미분하여 얻은 접선벡터 다발의 분포/벡터장(vector fields)이다. 이 벡터의 다발을 미분 연산자로 표현 벡터로 취급한다. 따라서 이 벡터장 비분 연산자는 벡터의 변환법칙을 따른다.]
벡터를 확장하면 기저벡터와 성분 곱의 선형조합이다. 기저벡터의 선택에 따라 성분이 달라진다. 이와 동일하게 (공간상에 움직이는) 벡터를 미분하여 접선 벡터를 구하면 다변수 편미분 연쇄법칙에 따라 선형조합의 꼴이 된다. 이 경우에도 (공간의)좌표계 선택에 따라 성분도 달라 진다. 벡터에 대해 공간축 편미분이 기저벡터에 해당하며 공간축에 대한 변화율이 그 성분이 된다.
-
-
일반화 한 선형 합을 아인슈타인 표기법(Einstein Summation Notation)으로 간략화 하여 기술하면 다음과 같다.
-
-
벡터 미분으로 접선벡터 다발(벡터장)을 구성하는 예를 보자. 길이가 2면서 회전운동을 하는 벡터 R을 미분한다. 벡터 R의 운동인자를 λ라 하자(물리학 이라면 시간 t라 했을 것). 벡터 R(λ)의 궤적을 직교좌표로 나타내면 (x(λ), y(λ)), 극좌표라면 (r(λ), θ(λ)) 가 된다. 직교좌표와 극좌표에서 기술된 기저벡터와 성분의 선형합을 비교해 보자. 운동의 형태에 따라 적절한 좌표계를 선택하면 벡터의 기술이 매우 단순해 진다. [직교좌표에서 두 초월함수였던 성분이 극좌표에서는 상수다! 그나마 한축의 성분은 0]
-
-
이번 강의에서 보이려는 것은 벡터 미분 성분이 반변한다는 점이다. 기초강좌에서 벡터 성분은 반변한다는 것을 배웠다. 반변(contra-variant)이란 순방향 변환 행렬로 변환되는 기저벡터 변환에 반해 성분은 역방향 변환 행렬이 사용된다는 의미이며 이를 그림으로 표현하면 기저벡터 크기를 늘이면 성분값은 반비례하여 작아진다는 뜻이다.
벡터 v는 기저벡터가 e_j인 좌표계 혹은 e_j_tilde 좌표계에서 저마다의 성분 값을 곱한 선형조합으로 표현된다. 두 좌표계사이에 호환되는 성분 값을 구해보면 서로 반변한다는 사실을 알 수 있다.
-
-
벡터장(vector fields)의 경우에도 동일한 반변 규칙이 적용된다. 변환행렬 대신 변미분 행렬(자코비언)이 곱해진다.
-
-
정리해보면 기저의 변환에 순방향, 성분의 변환에 역방향 변환행렬이 이용된다. 이를 서로 반대의 변환 도구(행렬 또는 자코비언)을 아용하므로 반변(contravariant) 한다고 한다.
-
-
지금배운 내용을 좀더 명확히 하기 위해 예제를 풀어보자.
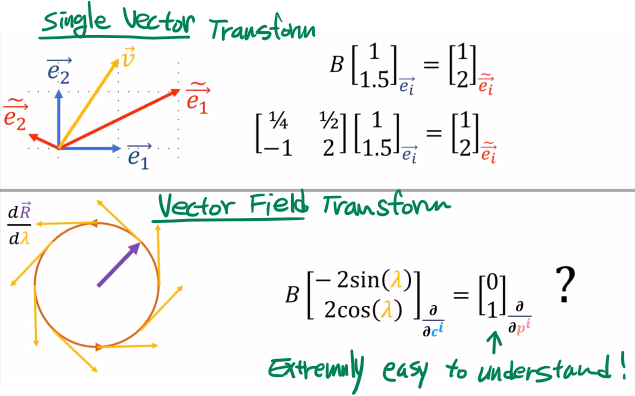
기저벡터가 e_i인 좌표계에서 벡터 v는 e_i_tilde로 변형된 좌표계에서도 변함이 없다(vector invariance). 하지만 두 좌표계에서 측정한 성분 값은 달라진다(component variance). 벡터 v의 원좌표계 성분 (1, 1.5)에 역방향 변환행렬 B을 곱하면 변형된 좌표계의 성분 (1,2)을 구할 수 있다. 두 좌표계에서 벡터 v의 성분이 값으로 알려져 있으므로 쉽게 계산할 수 있다.
이번에는 벡터장(vector field)의 경우를 보자. 직교좌표(Cartesian Coordinate)를 원좌표계로 두고 극좌표계(Polar Coordinate)를 변형좌표계라 하자. 벡터장은 벡터 R을 움직임 인자 λ에 대한 미분 dR/dλ 이다.
원운동을 하는 벡터 R 의 직교좌표계에서 성분은 초월함수로 표현된다. 그런데 극좌표 성분으로 표현하면 (0, 1) 이다. 도데체 역변환(미분)행렬(자코비언)이 어떻기에 이리 단순하게 되는 것일까?
-
-
벡터장의 변환은 미분연산 행렬이다. 직교좌표계에서 극좌표계로의 변환을 순방향으로 잡았다. 따라서 성분의 변환은 역방향 변환을 적용해야 한다. [직교좌표계 기저축을 'c' 라 하고 극좌표계 기저축을 'p'로 명명하였다. 그리고 변환은 기저축의 편미분 연산을 행렬로 표현한다. 순방향은 ∂c/∂p로 역방향은 ∂p/∂c 다. 외우기 좋게 분자에서 분로로 변환한다고 기억해 두자.]
-

-
위에서 구한 역 자코비언을 직교좌표계에서 벡터장의 성분과 곱하여 얻은 극좌표계에서의 벡터장 성분은 다음과 같이 계산된다.
-

-
이번에는 순방향 변환인 자코비언을 구해보자.
-

-
위의 자코비언을 곱하여 극좌표에서 벡터장 성분을 직교좌표계의 성분으로 변환하면 다음과 같다.
-

-
기초강좌에서 배웠던 벡터의 변환과 벡터장의 변환 과정이 같다는 것을 알 수 있다. [기저의 변환에 순방향, 성분의 변환에 역방향 적용]
-

-
지금까지 배운 내용을 정리해보자.
벡터(vector) v는 성분(component) v^i 과 기저벡터(basis vector) e_i 의 곱의 선형합(linear summation)으로 표현된다.
벡터장(vector field) dR/dλ 역시 위치 벡터(position vector) R에 대한 기저축 성분의 변화율 d(c^i)/dλ [또는 d(p^i)/dλ]과 기저축에 대한 접선벡터 ∂R/∂(c^i) [또는 ∂R/∂(p^i)] 곱의 선형 합으로 표현된다. 이때, 위치벡터는 좌표계의 각축 c^i 의 함수이므로 편미분(partial derivatives) 한다. 이 선형합은 다변수 미분의 연쇄법칙(chain rule of multi-variable derivatives)과 같으므로 특별히 외울 필요는 없을 것이다.
변형된 두 좌표계 사이의 변환규칙(transformation rules)은 성분과 기저벡터가 서로 반변(contra-variant)의 관계에 있다. 기저벡터 변환에 순방향 변환이 적용된다면 성분은 역방향 변환을 적용한다.
벡터장의 기저 ∂R/∂(c^i) [또는 ∂R/∂(p^i)]는 위치벡터 R에 대하여 기저축으로 편미분에 해당하며 위치벡터 일반에 적용되므로 편미분 연산자 ∂/∂(c^i) [또는 ∂/∂(p^i)] 만으로 표기한다.
-

-
앞으로 편미분 연산자를 기저벡터로 취급할텐데 생소하긴 하다. 익숙해지자.
-

-
How can a derivative operator can be considered a vector ?
먼저 지금까지 기저벡터라고 했던 벡터에 상수를 곱하거나 덧셈을 하는 벡터 연산이 미분연산자에 적용해도 그 성질이 유지된다는 점을 알고 시작하자.
-

-
그리고 미분은 한 점에서 기울기다. 기울기의 의미는 각 기저축의 크기에 영향을 준다. x축 편미분은 x축 방향을 취하고 y편미분은 y축 방향을 취한다. λ로 미분하면 결국 λ 방향을 취한다는 의미다. 따라서 미분은 일반적으로 벡터로서 받아들여지는 특성인 방향과 크기를 의미 한다고 할 수 있다.
-

-
또한 서로다른 좌표계의 각 기저축 간의 편미분은 자코비언 혹은 역 자코비언이라고 하는 변환에 이용된다는 점도 기억해 두자.
-

-
굳이 벡터 R의 표기를 생략하고 편미분 연산자만을 벡터로 취급하려는 이유는 위치벡터(position vector)를 다룰 것이기 때문이다. 벡터 R를 표시하면 원점이 있다는 전제하에 벡터를 그린다. 하지만 향후 다루게될 공간의 굴곡을 벡터로 표현할 때 원점의 개념은 없이 해당 지점에서 기저를 다루게 될 것이다. 앞선 강의에서 몇차례 이에대한 개념을 다뤘었다. 앞으로 공간의 휨을 기저의 변형이라는 '기괴한' 방식으로 점근할 것이다. 벡터의 움직임을 다룰때 공간, 즉 좌표체계를 동적으로 적용한다.
-

----------------------------------------------------------------
[이전] 4. 미분하면 벡터된다(Derivatives are Vectors)
-
벡터장의 변환은 미분연산 행렬이다. 직교좌표계에서 극좌표계로의 변환을 순방향으로 잡았다. 따라서 성분의 변환은 역방향 변환을 적용해야 한다. [직교좌표계 기저축을 'c' 라 하고 극좌표계 기저축을 'p'로 명명하였다. 그리고 변환은 기저축의 편미분 연산을 행렬로 표현한다. 순방향은 ∂c/∂p로 역방향은 ∂p/∂c 다. 외우기 좋게 분자에서 분로로 변환한다고 기억해 두자.]
-

-
위에서 구한 역 자코비언을 직교좌표계에서 벡터장의 성분과 곱하여 얻은 극좌표계에서의 벡터장 성분은 다음과 같이 계산된다.
-

-
이번에는 순방향 변환인 자코비언을 구해보자.
-

-
위의 자코비언을 곱하여 극좌표에서 벡터장 성분을 직교좌표계의 성분으로 변환하면 다음과 같다.
-

-
기초강좌에서 배웠던 벡터의 변환과 벡터장의 변환 과정이 같다는 것을 알 수 있다. [기저의 변환에 순방향, 성분의 변환에 역방향 적용]
-

-
지금까지 배운 내용을 정리해보자.
벡터(vector) v는 성분(component) v^i 과 기저벡터(basis vector) e_i 의 곱의 선형합(linear summation)으로 표현된다.
벡터장(vector field) dR/dλ 역시 위치 벡터(position vector) R에 대한 기저축 성분의 변화율 d(c^i)/dλ [또는 d(p^i)/dλ]과 기저축에 대한 접선벡터 ∂R/∂(c^i) [또는 ∂R/∂(p^i)] 곱의 선형 합으로 표현된다. 이때, 위치벡터는 좌표계의 각축 c^i 의 함수이므로 편미분(partial derivatives) 한다. 이 선형합은 다변수 미분의 연쇄법칙(chain rule of multi-variable derivatives)과 같으므로 특별히 외울 필요는 없을 것이다.
변형된 두 좌표계 사이의 변환규칙(transformation rules)은 성분과 기저벡터가 서로 반변(contra-variant)의 관계에 있다. 기저벡터 변환에 순방향 변환이 적용된다면 성분은 역방향 변환을 적용한다.
벡터장의 기저 ∂R/∂(c^i) [또는 ∂R/∂(p^i)]는 위치벡터 R에 대하여 기저축으로 편미분에 해당하며 위치벡터 일반에 적용되므로 편미분 연산자 ∂/∂(c^i) [또는 ∂/∂(p^i)] 만으로 표기한다.
-

-
앞으로 편미분 연산자를 기저벡터로 취급할텐데 생소하긴 하다. 익숙해지자.
-

-
How can a derivative operator can be considered a vector ?
먼저 지금까지 기저벡터라고 했던 벡터에 상수를 곱하거나 덧셈을 하는 벡터 연산이 미분연산자에 적용해도 그 성질이 유지된다는 점을 알고 시작하자.
-

-
그리고 미분은 한 점에서 기울기다. 기울기의 의미는 각 기저축의 크기에 영향을 준다. x축 편미분은 x축 방향을 취하고 y편미분은 y축 방향을 취한다. λ로 미분하면 결국 λ 방향을 취한다는 의미다. 따라서 미분은 일반적으로 벡터로서 받아들여지는 특성인 방향과 크기를 의미 한다고 할 수 있다.
-

-
또한 서로다른 좌표계의 각 기저축 간의 편미분은 자코비언 혹은 역 자코비언이라고 하는 변환에 이용된다는 점도 기억해 두자.
-

-
굳이 벡터 R의 표기를 생략하고 편미분 연산자만을 벡터로 취급하려는 이유는 위치벡터(position vector)를 다룰 것이기 때문이다. 벡터 R를 표시하면 원점이 있다는 전제하에 벡터를 그린다. 하지만 향후 다루게될 공간의 굴곡을 벡터로 표현할 때 원점의 개념은 없이 해당 지점에서 기저를 다루게 될 것이다. 앞선 강의에서 몇차례 이에대한 개념을 다뤘었다. 앞으로 공간의 휨을 기저의 변형이라는 '기괴한' 방식으로 점근할 것이다. 벡터의 움직임을 다룰때 공간, 즉 좌표체계를 동적으로 적용한다.
-

----------------------------------------------------------------
[다음] 5.1 Derivative Operators are Vectors Discussion
----------------------------------------------------------------
강의목차:
Tensor Calculus by eigenchris @ Youtube
0. 소개(Introduction)
1. 다변수 미적분 요약(Multi-variable Calculus Review)
2. 직각좌표계와 극좌표계 그리고 기저벡터(Cartesian & Polar Coordinates, and Basis Vectors)
3. 자코비언(The Jacobian)
4. 미분하면 벡터된다(Derivatives are Vectors)
5. Derivative Transformation Rules (Contravariance)
5.1 Derivative Operators are Vectors Discussion
6. Differential Forms are Covectors
7. Covector Field Components
8. Covector Field Transformation Rules (Covariance)
9. Integration with Differential Forms
10. Integration with Differential Forms Examples
11. The Metric Tensor and Arc Lengths (flat space)
12. The Metric Tensor in Curved Spaces for Measuring Arc Length
13. Gradient vs d operator (exterior derivative_differential)
14. Gradient explanation + examples
15. Geodesics and Christoffel Symbols (extrinsic geometry)
16. Geodesic Examples on Plane and Sphere
17. The Covariant Derivative (flat space)
17.5 Covariant Derivative (Component Definition) - Optional
18. Covariant Derivative (extrinsic) and Parallel Transport
19. Covariant Derivative (Intrinsic) and Geodesics
20. The Abstract Covariant Derivative (Levi-Civita Connection)
21. Lie Bracket, Flow, Torsion Tensor
22. Riemann Curvature Tensor Geometric Meaning (Holonomy + Geodesic Deviation)
23. Ricci Tensor Geometric Meaning (Sectional Curvature)







댓글 없음:
댓글 쓰기