1주: 물질과 힘 그리고 측정(Matter and forces, measuring and counting)
W1.0 환영(Welcome)
W1.1 물질(Matter)
W1.2 힘(Forces)
W1.2a 자연단위(Natural units)
W1.2b 특수 상대론과 4-벡터(Special relativity and four-vector)
W1.2c 가상입자(Virtual Particles)
W1.3 확률과 단면(Probability and cross section)
W1.3a 광자 빔의 감쇄(Attenuation of a photon beam)
W1.4 러더포드 실험(Rutherford experiment)
W1.4a 러더포드 단면(Rutherford cross section)
W1.4b 산란율 계산(Counting rate Rutherford)
W1.5 양자 산란(Quantum scattering)
W1.6 러더포드 실험 실습(Rutherford experiment in practice)
W1.7 1주 평가문제(Graded quiz for module 1)
2주: 핵 물리학(Nuclear Physics)
W2.1 핵 질량 및 결합 에너지(Nuclear mass and binding energy)/동영상/영문자막/슬라이드
[2.1-1] -------------------------------------------------------------

During this module, we'll deal with nuclear physics and its applications.
둘째주 강의의 목표는 핵물리(nuclear physics)와 그 응용을 다뤄본다
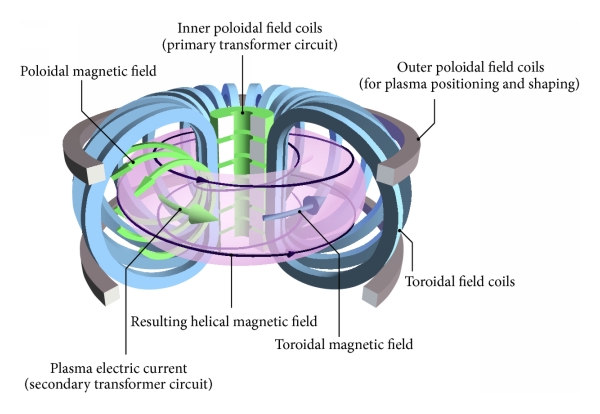
At the end of the module, we will visit the Tokamak of the Swiss Institute of Technology in Lausanne. And the Beznau Nuclear Power Plant which is the oldest one still in operation.
로잔에 있는 스위스 기술원(Swiss Institute of Technology)의 토카막(Tokamak)을 방문해보자. 그리고 가장 오래됀 핵발전 시설중 여전히 가동중인 베즈노(Beznau power plant)를 방문한다.
This is pretty much a self-contained module, if your main interest is nuclear physics, you will be well-served. You will also notice that it is somewhat longer than other modules, so just take your time to digest the contents without pressure.
이번주 강의분은 자습 과정이 많이 포함돼어 있다. 핵물리학에 관심이 있다면 도움이 될 것이다. 다른 주에 비해 분량이 좀 많아 보이지만 부담갖지말고 요약해서 보도록 하자.
In this first video, we will review what is known about the mass of nuclei. The goals for you are the following.
이번주 첫 강의를 마치면 배우게 될 것들,
- To know the nomenclature of atomic nuclei and their periodic system.
원자핵의 분류(명명, nomenclature)과 주기율표(peoridic system)
- To be able to qualitatively describe the mass and binding energy of nuclei.
핵의 질량과 결합 에너지를 정량적으로 이해
[2.1-2] -------------------------------------------------------------

Experiments of the Rutherford type demonstrate the existence of a positively charged nucleus, which is four orders of magnitude smaller than the size of the atom. These experiments only require to understand electromagnetic interactions between the project and the target.
러더포드 실험 유형(산란실험)으로 알 수 있는 것은 크기가 원자의 만분의 일(four order of magnitude) 가량되는 크기로 양(전기)으로 하전된 핵이 존재한다는 점. 이런 류의 산란실험(scattering)은 단지 입사입자(projectile)와 목표입자(target) 사이에 전자기적 작용(electromagnetic interaction) 정도를 이해할 수 있다.
Scattering experiments can also yield information about nuclear properties. And thus establish a catalog of the properties of the nuclear interaction that holds together protons and neutrons inside the nucleus.
산란실험을 통해 핵의 특성에 관한 정보가 드러나는데, 그를 토대로 양성자(proton)와 중성자(neutron)가 결합된 핵(nucleus)의 특성을 토대로 목록을 만들어 봤다.
One must not confuse this nuclear force with the strong force introduced in the first module and more extensively discussed in module number five.
이 (양성자와 중성자들을 묶어놓은)핵력(nuclear force)은 앞서 선보였던 강력(strong force)와 다른 것이다. 강력에 대해서는 5주째에 자세히 다루겠다.
The strong force binds together quarks inside hadrons by gluon exchange. It does not permit quarks to leave the hadrons.
강력(the strong force)은 강입자(hadron)내부에서 글루온(gluon)의 (에너지)전환으로 쿼크(quark)들을 묶어놓는 힘이다. 즉, 쿼크들이 강입자 밖으로 빠져 나가지 못하게 잡아둔다.

So hadrons in general and nucleons in particular, do not carry a net color charge. Thus gluons cannot bind protons and neutrons to form a nucleus.
일반적인 강입자(hadron)와 특별한 핵자(nucleon)는 총색전하(net color charge)를 갖지 않는다. 따라서 양성자(proton)와 중성자(neutron)를 묶어 핵을 형성하는데 글루온이 역활을 하는 것이 아니다.
The nuclear force is more like a long distance residue of the strong force in that it resembles the well-known Van der Waals force, which is a residue of the electromagnetic interaction which acts between electrically neutral molecules.
핵력(the nuclear force)은 강력(the strong force)처럼 작용 범위가 넓은데 마치 전기적으로 중성인 분자들 사이에 전자기 작용을 설명하는 반 데르 발스 힘(Van der Waals force)과 비슷하다.
[2.1-3] -------------------------------------------------------------

Let us compare some basic properties of atoms, and the electromagnetic force on one side, to nuclei, and the nuclear force on the other side.
전자기력(electromagnetic force)이 지배하는 원자(atom)와 핵력(nuclear force)이 우세한 핵(nuclei)을 비교해본다.
The electromagnetic force is responsible for holding atoms together. Its properties are well known, classically, and rather easy to extrapolate to quantum distances. The study of atomic spectra indeed gave rise to quantum mechanics, which qualitatively and quantitatively explains many phenomena of condensed matter physics. The fine structure constant, the electromagnetic coupling constant, is a small number, α≊1/137, which makes perturbative calculations feasible.
전자기력(The electromagnetic force)은 원자를 묶어놓는다. 전자기력은 양자 거리에서 벗어난 규모에서 고전적으로 잘 알려져 있다. 사실 원자 스펙트럼(E=ħν)을 연구하는 과정에서 양자역학의 계기가 되었다. 이는 미세물질(아원자 물리학) 물리학(fine matter physics)의 여러 현상들을 잘 설명한다. 미세구조상수(fine structure constant) 혹은 전자기 결합상수(Coupling constant)가 α≊1/137 가량으로 매우 작아서 섭동이론(Perturvation theory) 적 계산이 유효하다.
The nuclear force, on the other hand, must be much stronger, since it wins over the Coulomb repulsion between tightly-packed protons. It must be of short range, since it doesn't make itself felt outside the nuclear volume. It has no classical analog. Only experimental results can help to understand its properties. One thus uses experiments as a guide towards empirical models of the nucleus and of the nuclear force. We will come back to the relation between experiments and models as we go along.
핵력(The nuclear force)은 한편 쿨롱 반반력을 넘어 양성자들을 서로 가깝게 묶어둘수 있을 정도로 훨씬 강력한 힘이다. 아주 좁은 범위에서 작동하며 핵 이외의 영역에 미치지 못한다. 핵력은 고전물리 설명될 수 없고 오직 실험적으로 그 특성을 이해할 수 있다.
[2.1-4] -------------------------------------------------------------

Let us first summarize how we identify and denote nuclei.
- 'Z', the nuclear charge, which is equal to the atomic number in the periodic table. It is given by the number of protons in the nucleus.
Z는 핵의 전하값으로 양성자의 수(number of proton)로 결정된다. 주기율표(ptable.com)의 원자번호(atomic number)에 해당한다.
- 'A' is the number of nucleons, the sum of protons and neutrons, it is also called the mass number.
A는 핵자(nucleons)의 수로 양성자와 중성자를 더한 값이다. 핵의 질량수(mass number)라고 하기도 한다.
- Nuclei are thus completely identified by their electric charge and the number of nucleons. The name we give them identifies Z and usually is supplemented by A. When we say carbon 14, that means a nucleus with Z=6 and A=14.
핵(Nucleus)은 하전량과 핵자의 수에 따라 분류된다. 즉, 원자는 이름에 Z 와 A 수가 따라 붙는다. 예를 들어 탄소14라고 한다면 핵에 Z=6이고 A=14라는 뜻이다.
- Evidently, the number of neutrons is then the difference between the mass number and the atomic number, and is denoted by N.
중성자(neutrons)의 수는 질량수와 원자번호에서 구할 수 있는데 N으로 표기한다. 질량수와 원자번호의 차이가 바로 중성자 수다.
- The chemical properties of the elements are determined by the electron cloud surrounding the nucleus. The periodic table is thus organized according to Z.
원소의 화학적 특성은 핵을 둘러싼 전자구름에 의해 결정된다. 주기율표는 Z로 구성한다. 원자는 하전수(양성자의 수)인 Z에 따라 구분된다.
- Nuclei with the same number of protons, but with a different number of neutrons, are called isotopes. They have very similar chemical properties but not necessarily similar nuclear properties.
핵이 동일한 개수의 양성자를 가졌으나 중성자의 수가 다른 경우를 동위원소(isotope)라고 한다. 이 원소들은 화학적 특성이 비슷하나 핵의 특성이 꼭 같다고 할 수는 없다.
Examples are uranium 235 and uranium 238, which have both 92 protons, but a different number of neutrons and thus different stability properties. Another example is hydrogen, deuterium, and tritium which all have one proton and zero, one, or two neutrons.
예를 들어 우라늄 235와 우라늄 238은 모두 양성자가 92 이지만 중성자의 수가 서로 다르며 그에따라 안정 특성이 다르다(핵이 쉽게 붕괴될 수 있음). 또다른 예로 수소가 있는데, 중수소() 삼중수소()로 불리우는 경우다. 각각 모두 한개의 양성자를 가지고 있지만 중성자의 수가 없거나 한개 혹은 두개를 가지고 있는 경우다.
- Nuclei can also be excited to higher states, keeping the number of protons and neutrons constant. These are called resonances or isomers.
핵이 동일한 양성자와 중성자를 가졌더라도 활성(be excited)상태에 있을 수 있는데 이를 이성질체(resonances or isomers)라고 한다.(양성자와 중성자의 배열, 결합이 다름)
- Nuclei with the same number of nucleons but the different number of protons are called isobars. They have roughly the same nuclear mass. Examples are carbon 12 and boron 12, with both have 12 nucleons.
중성자가 동일하면서 양성자가 다른 경우를 동중원소(isobar)라고 부른다.
[2.1-5] -------------------------------------------------------------

- Naively one might assume that the mass of nuclei is simply given by the sum of the masses of protons and neutrons they contain. But in reality, this mass is, of course, diminished by the binding energy between the nucleons.
핵의 질량(nuclear mass, A)를 단순히 양성자(Proton)와 중성자(Neutron)의 합(A=N+Z)이라고 하지만 엄밀히 말하자면 틀리다. 실제 핵의 질량에는 핵자들의 질량과 그들 사이의 결합 에너지(binding energy)를 포함하고 있다.

- The mass deficit ∆M must always be negative so that the nucleus is in a bound state. We call it the binding energy. It has been measured for practically all nuclei.
핵자(nucleons)의 질량(양성자와 중성자의 질량을 같게 놓은 핵의 질량)과 실제 핵의 질량, (Z*m_p) + (N*m_n) 의 차 ∆M은 0보다 작은데 이로인해 핵이 정상상태에 머무르게 한다.
- The absolute value of the binding energy is the energy required to decompose the nucleus into separate nucleons.
이 질량차 ∆M의 절대값을 결합 에너지라 한다. 역으로 핵자들을 분리하는데 필요한 에너지이기도 하다.

- The binding energy per nucleon, ∆M/A, is the energy required to separate the average nucleon from its nucleus. It is much smaller than the mass of a nucleon p and n. The mass of the nucleus is thus indeed dominated by the mass of its constituents.
핵자 당 결합 에너지 ∆M/A 는 핵에서 핵자 하나를 떼어내는 에너지라 할 수 있다. 이 에너지는 핵자인 p (양성자) 와 n (중성자)의 질량보다 아주 작다. 핵의 질량은 대부분 이들 핵자들의 질량이 차지한다.
- For the nucleons themselves the situation is very different. The total mass of the quarks inside the nucleon is only around 1% of the nucleon mass. It is their binding energy which dominates the nucleon mass.
핵자 하나하나의 질량을 따져보면 좀 다르다. 핵자의 내부를 구성하는 쿼크의 무게는 핵자의 무게에 1%에 지나지 않는다. 결합 에너지가 핵자 무게의 상당부분을 차지한다.
[2.1-6] -------------------------------------------------------------

When one analyzes the dependence of the binding energy, ∆M per nucleon A, on the mass number A one notices the following.
질량수 A와 핵자당 결합 에너지 ∆M/A의 상관관계를 보자.
- For A less than 20 on the left side of this graph, ∆M/A oscillates but rises rapidly with increasing A.
A가 20 이하인 구간에 놓인 원소들인 경우 ∆M/A가 들쭉날쭉 하지만 급격히 증가한다.
- For A between 20 and 60, ∆M/A saturates. For A about 60, it has a broad maximum. That is, the iron group formed by nickel, iron, and cobalt with about 9 MeV per nucleon of binding energy.
- For A larger than 60, the binding energy per nucleon decreases slowly.
질량수 A가 60을 넘는 원소의 경우 결합 에너지는 다소 감소하지만 여전히 매우 높음을 유지한다.
The general mean is about 8 MeV per nucleon. The kinetic energy of nucleons inside the nucleus must thus be relatively small. Otherwise, they would not stay bound. The velocities of bound nucleons are thus non-relativistic.
[2.1-7] -------------------------------------------------------------

The binding energy corresponds indeed to a wavelength of nucleons inside the nucleus. This wavelength is less than two Fermi of the order of the nucleus' size itself. It is thus plausible that the nucleus can contain nucleons with the maximum kinetic energy of about 8 MeV. Or a maximum momentum of about 120 MeV.
If, on the other hand, the nucleus would contain electrons, they would be relativistic and their wavelength would be 2.5 x 10^-12 centimeters, much bigger than the nucleus size. The nucleus can thus not contain bound electrons. They need a much larger volume to be contained. This is obviously in agreement with the findings of Geiger and Marsden, that we have discussed in the previous module.
In the next video, we will talk about the size and the spin of nuclei.
[연습문제]-----------------------------------------------------------




댓글 없음:
댓글 쓰기